前言
BP算法作为神经网络的经典算法,理解其原理非常重要,我将从原理开始讲起,然后过渡到代码实现。
一:BP算法
1.1 反向传播算法和 BP 网络简介
误差反向传播算法简称反向传播算法(即 BP 算法)。反向传播算法于1986 年由 David E. Rumelhart和 James L. McClelland 发表于书籍 Parallel Distributed Processing 中。使用反向传播算法的多层感知器又称为 BP 神经网络。
BP 算法是一个迭代算法,它的基本思想为:
(1) 先计算每一层的状态和激活值,直到最后一层(即信号是前向传播的);
(2) 计算每一层的误差,误差的计算过程是从最后一层向前推进的(这就是反向传播算法名字的由来);
(3) 更新参数(目标是误差变小),迭代前面两个步骤,直到满足停止准则(比如相邻两次迭代的误差的差别很小)。
下面以三层感知器(即只含有一个隐藏层的多层感知器)为例介绍“反向传播算法(BP 算法)”。
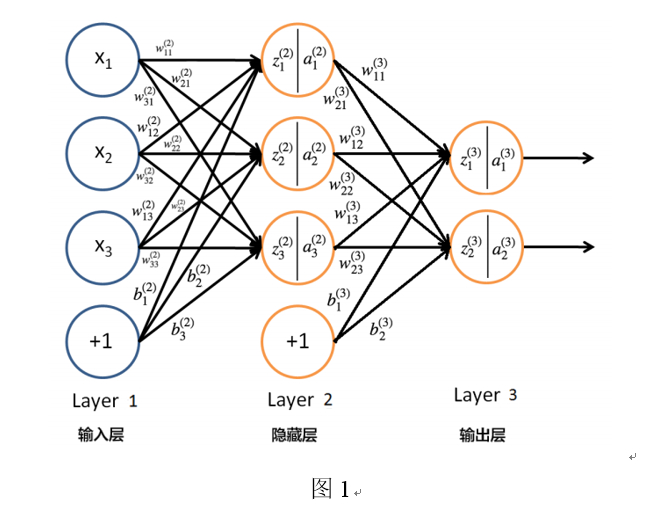
三层感知器如图 1 所示。例子中,输入数据 $X=\left(x_1,x_2,x_3\right)^T$是 3 维的。对于第一层,可以认为$(a_i^1=x_i)$唯一的隐藏层有 3 个节点,输出数据是 2 维的。
1.2 信息前向传播
显然,图 1 所示神经网络的第 2 层神经元的状态及激活值可以通过下面的计算得到:
类似地,第 3 层神经元的状态及激活值可以通过下面的计算得到:
可总结出,第$l\left(2\le l\le L\right)$层神经元的状态及激活值为(下面式子是向量表示形式):
对于$L$层感知器,网络的最终输出为 $a^L$。前馈神经网络中信息的前向传递过程如下:
1.3 误差反向传播
“信息前向传播”讲的是已知各个神经元的参数后,如何得到神经网络的输出。但怎么得到各个神经元的参数呢?“误差反向传播”算法解决的就是这个问题。假设训练数据为$\left(x^1,y^1\right),\left(x^2,y^2\right),\ldots\left(x^i,y^i\right),\ldots,\left(x^N,y^N\right)$,即输入数据为N维。又假设输出数据为$n_L$维,即,网络输出为$z^i$。此时对于某一层数据$\left(x^i,y^i\right)$来说,其误差计算函数可以用标准差函数表示:
显然总体误差可以表示为
我们的目标是调整权重和偏置函数使总体误差变小,求得当总体误差最小时对应的各神经元的参数(权重和偏置)。
采用常见的梯度下降法,可以用下面公式更新参数$W_{ij}^l$,$b_i^l$,$2\le l\le L$:
由上式推导可知,只要知道每一个训练数据的误差$E_i$对参数的偏导数 ,即可得到参数的迭代更新公式。
1.3.1权重参数更新
对于所有有输入的层,包括中间层和输出层为表示方便,设E=Ei,y=yi,z=zi,都有:
以图1 Layer3 z1为例
对其求偏导,有:
如果我们把$\frac{\partial E}{\partial z_i^l}$记为$\delta_i^l$,即:
则$\frac{\partial E}{\partial w_{11}^3}$可以表示为:
在layer2 z1中同理也有
其中我们发现,BP网络是全连接的,即若对$\delta_i^j$向后展开,可以得到:
上式是BP算法的核心,它利用第l+1层的$\delta_j^{l+1}$计算第l层的$\delta_j^l$,也是“误差反向传播算法”的名字由来。
1.3.2偏置参数更新
1.3.3 BP网络的四个核心算法
2 python代码实现BP算法
通过上面数学推导,我们已经知道关键参数如何设置,废话不多说,直接上代码1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179# -*- coding: utf-8 -*-
"""
Created on Fri Jun 7 09:20:40 2019
@author: lei
"""
import math
import random
import pickle
random.seed(0)
def rand(a, b):
return (b - a) * random.random() + a
def make_matrix(m, n, fill=0.0):
mat = []
for i in range(m):
mat.append([fill] * n)
return mat
def sigmoid(x):
return 1.0 / (1.0 + math.exp(-x))
def sigmoid_derivative(x):
return x * (1 - x)
class BPNeuralNetwork:
def __init__(self):
self.input_n = 0 #输入层数量
self.hidden_n = 0 #隐藏层
self.output_n = 0 #输出层
self.input_cells = [] #输入矩阵
self.hidden_cells = [] #隐藏层矩阵
self.output_cells = [] #输出矩阵
self.input_weights = [] #输入权重矩阵
self.output_weights = [] #输出权重矩阵
self.input_correction = [] #输入矫正矩阵
self.output_correction = [] #输出矫正矩阵
self.train_acc = .0 #训练集准确率
self.test_acc = .0 #测试集准确率
def setup(self, ni, nh, no):
self.input_n = ni + 1
self.hidden_n = nh
self.output_n = no
# init cells
self.input_cells = [1.0] * self.input_n #输入层节点初始化
self.hidden_cells = [1.0] * self.hidden_n #隐藏层节点初始化
self.output_cells = [1.0] * self.output_n #输出层节点初始化
# init weights
self.input_weights = make_matrix(self.input_n, self.hidden_n)
#输入层权重初始化
self.output_weights = make_matrix(self.hidden_n, self.output_n)
#输出层权重初始化
# 随机填充参数
for i in range(self.input_n):
for h in range(self.hidden_n):
self.input_weights[i][h] = rand(-0.2, 0.2)
for h in range(self.hidden_n):
for o in range(self.output_n):
self.output_weights[h][o] = rand(-2.0, 2.0)
# 初始化矫正矩阵
self.input_correction = make_matrix(self.input_n, self.hidden_n)
self.output_correction = make_matrix(self.hidden_n, self.output_n)
def predict(self, inputs):
# 激活输入层
for i in range(self.input_n - 1):
self.input_cells[i] = inputs[i]
# 激活隐藏层
for j in range(self.hidden_n):
total = 0.0
for i in range(self.input_n):
total += self.input_cells[i] * self.input_weights[i][j]
self.hidden_cells[j] = sigmoid(total)
# 激活输出层
for k in range(self.output_n):
total = 0.0
for j in range(self.hidden_n):
total += self.hidden_cells[j] * self.output_weights[j][k]
self.output_cells[k] = sigmoid(total)
return self.output_cells[:]
def back_propagate(self, case, label, learn, correct):
# 前向反馈
self.predict(case)
# 得到输出层误差
output_deltas = [0.0] * self.output_n
for o in range(self.output_n):
error = label[o] - self.output_cells[o]
output_deltas[o] = sigmoid_derivative(self.output_cells[o]) * error
# 得到隐藏层误差
hidden_deltas = [0.0] * self.hidden_n
for h in range(self.hidden_n):
error = 0.0
for o in range(self.output_n):
error += output_deltas[o] * self.output_weights[h][o]
hidden_deltas[h] = sigmoid_derivative(self.hidden_cells[h]) * error
# 更新输出权重
for h in range(self.hidden_n):
for o in range(self.output_n):
change = output_deltas[o] * self.hidden_cells[h]
self.output_weights[h][o] += learn * change + correct * self.output_correction[h][o]
self.output_correction[h][o] = change
# 更新输入权重
for i in range(self.input_n):
for h in range(self.hidden_n):
change = hidden_deltas[h] * self.input_cells[i]
self.input_weights[i][h] += learn * change + correct * self.input_correction[i][h]
self.input_correction[i][h] = change
# 得到全局误差
error = 0.0
for o in range(len(label)):
error += 0.5 * (label[o] - self.output_cells[o]) ** 2
return error
def get_precise_rate(self,cases,labels):
#得到结果准确率
right_num=0
length=len(labels)
for i in range(length):
predict=self.predict(cases[i])
predict.index(max(predict))
#返回最大可能的索引值,所以只支持one Hot编码模式
if predict.index(max(predict))==labels[i].index(max(labels[i])):
right_num+=1
return right_num/length
def train(self, train_list, test_list, limit=10000, learn=0.05, correct=0.1):
self.train_acc=.0
self.test_acc=.0
for j in range(limit):
error = 0.0
for i in range(len(train_list[0])):
label = train_list[1][i]
case = train_list[0][i]
error += self.back_propagate(case, label, learn, correct)
#print("第%d轮,训练次数:%d"%(j,i),end='\r')
self.train_acc=self.get_precise_rate(train_list[0],train_list[1])
self.test_acc=self.get_precise_rate(test_list[0],test_list[1])
print("训练次数:%d,train_acc:%f,test_acc%f"%(j,self.train_acc,self.test_acc),end='\r')
def save(self,fliename):
f=open(fliename,'wb')
pickle.dump(self, f)#使用python自带pickle模块保存
f.close()
def load(self,fliename):
f = open(fliename, 'rb')
return pickle.load(f)#返回模型
def test(self):
#一个简单的异或学习例子
cases = [
[0, 0],
[0, 1],
[1, 0],
[1, 1],
]
labels = [[0], [1], [1], [0]]
self.setup(2, 5, 1)
self.train(cases, labels, 10000, 0.05, 0.1)
for case in cases:
print(self.predict(case))
if __name__ == '__main__':
nn = BPNeuralNetwork()
nn.setup(20,200,3)
nn.train(x)
nn.test()
利用python自带库完整实现一个三层的BP神经网络,可以支持保存,加载等常见操作,由于时间有限,水平有限,目前不支持添加多层隐藏层。以后再来填坑把。
参考
